
円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
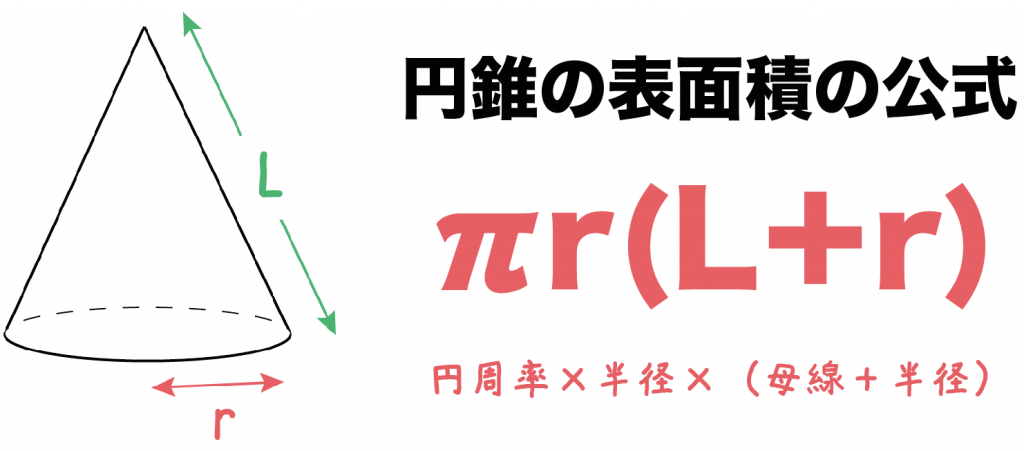
円錐の側面積を求める公式より、 円錐の側面積 = 母線 × 半径 × 円周率 = 8cm × 3cm × π = 24 π cm 2 扇形の面積を求める公式を導出する 円錐の側面積 = LRπ で求めることができることがわかりましたが、この式を変形してみます。これを側面積の式に代入すると、 『側面積=母線×底面の半径×\(\pi\)』 という公式が導けます。 ただあまり語呂が良くないので、視覚的に「こことここをかけたら側面積になる」という風に覚えるほうが良いでしょう。
円錐 側面積 公式 なぜ
円錐 側面積 公式 なぜ-ここから、円錐台の側面積は、大小二つの 円錐の側面積 の差として、計算できます。 ですが、これで終わりではありません。 この式では、大小二つの円弧の半径である l 1 、 l 2 を別に求めておかないと計算できず、実際に使用するにはやや不便です。 そこで、もっと簡単に扱えるように、これをあらかじめ組み込んで、さらに公式を作り込みます。 目標は まとめ:円錐関連の公式 母線, 底面の半径, 側面の扇形の中心角として, 円錐の側面積 の公式 円錐の表面積 の公式 (表面積) (側面積) (底面積) 側面のおうぎ形の中心角 に関しては という公式があるが, 登場は の方が使用頻度は高いと思われるので割愛している。 では例題をやってみよう。
Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ
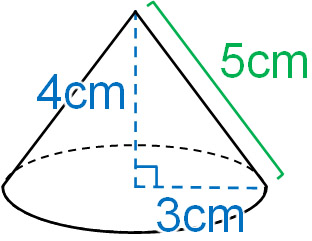
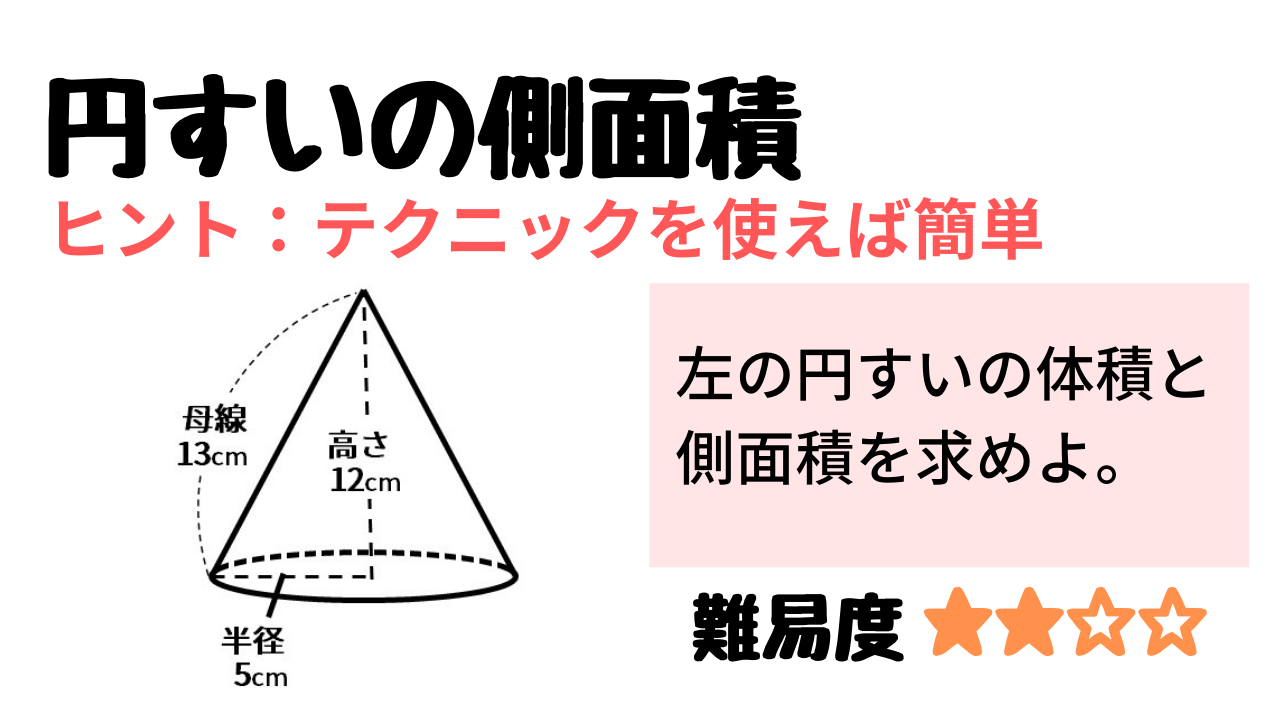
円錐の体積の公式は、 V = 1 3 πhr2 V = 1 3 π h r 2 だから、高さ = 9 = 9 , 半径 = 5 = 5 を代入して、 V = 1 3 × π ×9 × 52 = 75π V = 1 3 × π × 9 × 5 2 = 75 π だね! はかせちゃん あっさりしすぎたかな お疲れ様でした~ 関連記事はこちら 中学数学円錐の表面積 続いて表面積です。 円錐の表面積の公式は「底面積 側面積」でしたね。 底面積は6 × 6 × π = 36π とすぐに出せますね。 続いて、円錐の側面積の求め方は「半径 × π(半径 母線)」でしたね。 よって、側面積の式は 6π(6 10)= 96π となります。 なので、本日は、ぜひアナタに円すいの問題を解けるようになっていただけたらと思います。 円すいの体積を求める公式は 底面積×高さ÷3 です。 昨日紹介した 角すいの体積の公式 と同じですね。 つまり、角すいや円すいは「底面積×高さ÷3」で求める
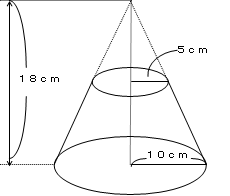
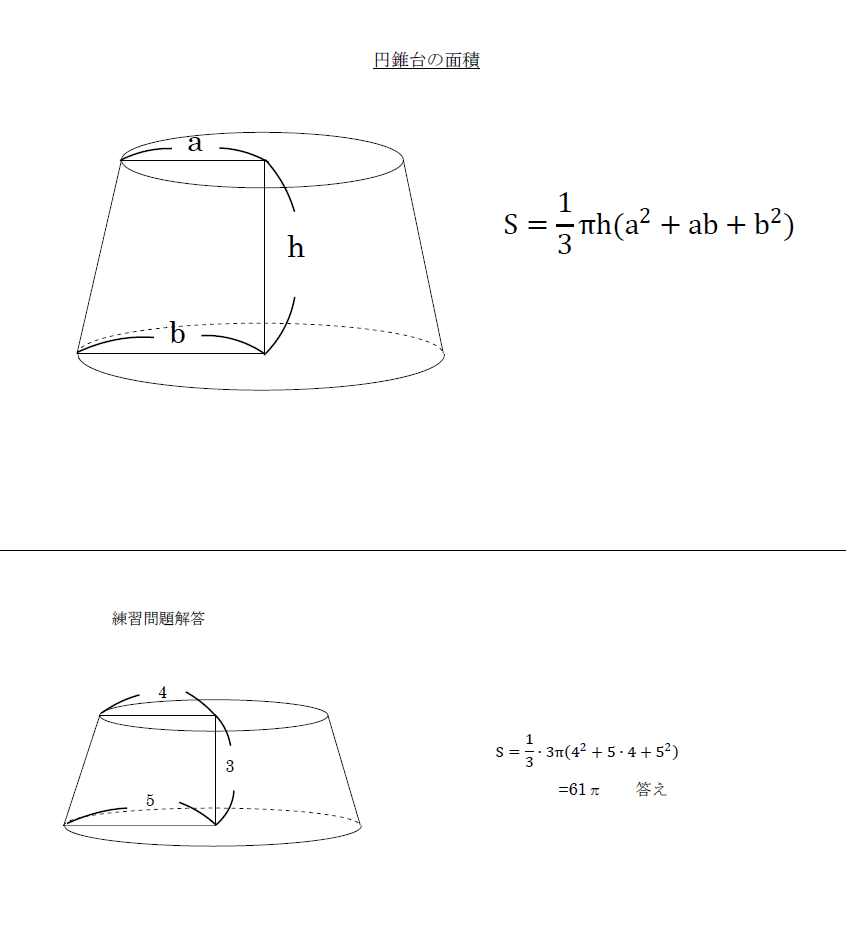
直円錐台の側面積 両底面の半径がそれぞれr1,r2で、母線の長さがl である直円錐台の側面積S は S = pl r1 r2 である。 証明 図の直円錐台の展開図を考える。AB, A'B' の延長の交点をO,頂角の大きさをa OA= R1, OB = R2とする。展開図の弧AA' は A r1 直円錐台の上の円周に等しいから、 円錐の側面積・表面積・体積 円錐に関しては少しややこしくなります。 まず側面積ですが、これは母線の長さがmで、扇形の面積になります。 具体的な証明については省きますが、側面積は「1/2 × 弧AB × 母線」となるので、 1/2*(m*2πr)=πmr となります。 一方で円柱の場合、側面積は1つの長方形と見なすことができます。 (縦=高さ、横=円周の長さ) なので、立体によって公式は同じでも、側面積の求め方が異なることは理解しておきましょう。 角錐と円錐の表面積
円錐 側面積 公式 なぜのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 | 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 | 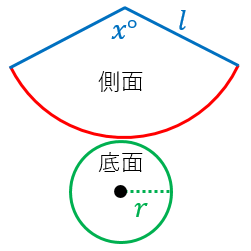 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
「円錐 側面積 公式 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 | 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
「円錐 側面積 公式 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 | 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 | 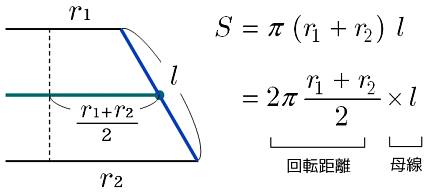 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
「円錐 側面積 公式 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 | 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 | 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
「円錐 側面積 公式 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 | 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
「円錐 側面積 公式 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 | 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 | 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 | 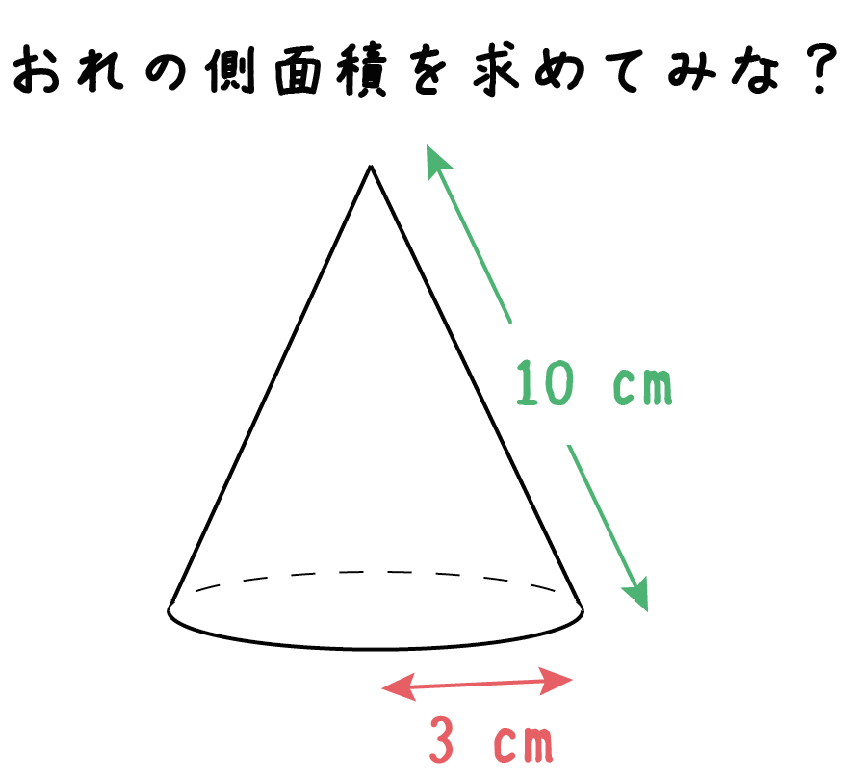 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
「円錐 側面積 公式 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 | 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 | 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
「円錐 側面積 公式 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 | 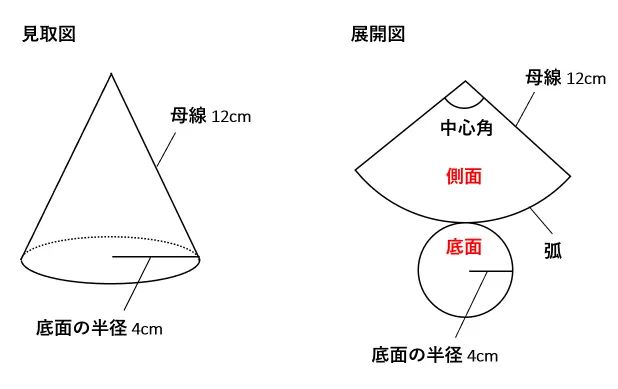 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
「円錐 側面積 公式 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 | 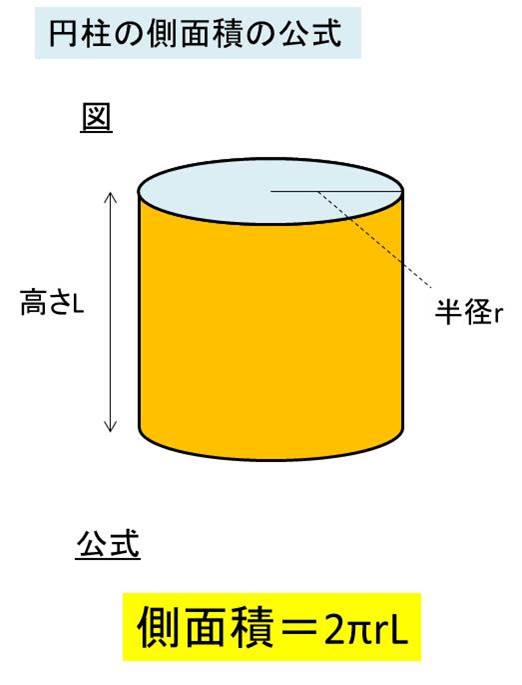 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
「円錐 側面積 公式 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 | 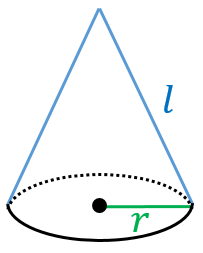 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 | 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
「円錐 側面積 公式 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
 円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |  円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学 |
円錐の公式(計算式) 体積V表面積S側面積F半径r母線R 体積V V = 1 3 π r 2 h 表面積S S = π r r R 側面積F F = π R rよって、円錐の側面積は「扇形の面積」です。 扇形の面積の公式は「r 2 θ/2(=半径×半径×中心角÷2)」です。rは扇形の半径(母線)、θは扇形の中心角(単位はラジアン)です。つまり、r 2 θ/2を算定すれば円錐の側面積が得られますが、θを使わずに側面積が算定できるとより簡単です。
Incoming Term: 円錐 側面積 公式, 円錐 側面積 公式 なぜ,




0 件のコメント:
コメントを投稿